線形回帰分析とは？やり方から活用法まで徹底解説
momeq
AI Master
Excelでできる！住宅価格データの線形回帰分析入門【初心者向け】
momeq
**「線形回帰分析って難しそう…」**と思っていませんか？
実は、お馴染みのExcelを使えば、プログラミングの知識がなくても本格的な統計分析ができるんです。今回は、住宅価格データを使って、面積や部屋数などの条件が価格にどう影響するかを分析してみましょう。
線形回帰分析って何？
線形回帰分析とは、「AがBに与える影響の大きさ」を数値で表す統計手法です。
例えば：
- 「面積が1㎡増えると、価格は何万円上がる？」
- 「築年数が1年増えると、価格は何万円下がる？」
こういった関係性を、データから客観的に読み取ることができます。
線形って、直線のことだよね？でも不動産価格って曲線的に変化しそうだけど…
確かに現実は複雑だけど、線形回帰でも十分実用的な結果が得られることが多いんだ。まずは線形から始めて、必要に応じて曲線回帰も試してみよう。
準備：サンプルデータについて
今回使用するのは、架空の住宅価格データです。以下の項目が含まれています：
| 列名 | 説明 |
|---|---|
area_sqm | 専有面積（㎡） |
rooms | 部屋数 |
age_years | 築年数 |
station_distance_min | 最寄り駅からの距離（分） |
floor | 階数 |
price_million_yen | 価格（万円）← 目的変数Y、これを予測したい |
今回使用するデータです。csvファイルですので、良かったらこちらを利用してみてください。
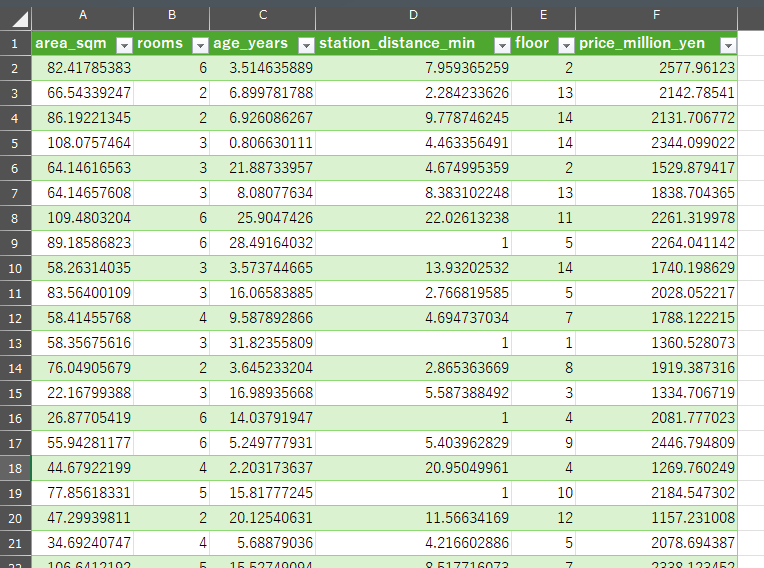
どんな感じのデータか教えて。
次がデータの詳細だよ、最小、最大、平均、中央値を列挙してあるよ。例えば部屋数であれば、最小で１部屋、最大で６部屋、平均で３．５４部屋、中央値は３部屋って感じかな。
| 変数名 | 最小値 | 最大値 | 平均 | 中央値 |
|---|---|---|---|---|
| area_sqm | 20.658006 | 149.085423 | 84.813023 | 86.711287 |
| rooms | 1.000000 | 6.000000 | 3.534000 | 3.000000 |
| age_years | 0.011876 | 49.967675 | 25.937612 | 26.498170 |
| station_distance_min | 1.009643 | 29.868934 | 15.197620 | 15.179237 |
| floor | 1.000000 | 14.000000 | 7.462000 | 7.000000 |
| price_million_yen | 506.648657 | 2989.904066 | 1749.926 | 1733.422 |
ステップ1：データの読み込み
まずは、ExcelにCSVデータを読み込みましょう。そのままCSVを開いてもいいけど、文字化けすることあるので、今回はExcelのデータから開きます。
Excelを開く
まずは、PC内でインストールされているExcelを開いてください。
「データ」タブ → 「テキストまたはCSVから」を選択
リボンのデータタブ内にある「テキストまたはCSVから」を選択して、対象のファイルを選んで「インポート」を押してください。
対象のCSVファイルを選んで読み込み
今回はそのまま読み込めそうなので読み込みを押して、データを読み込めば反映されます。
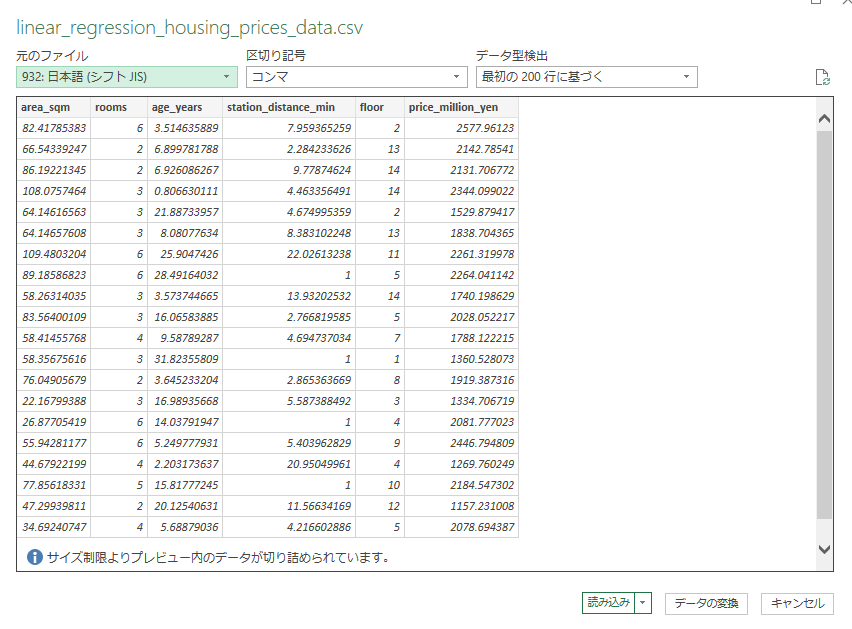
※バージョンによって使えなかったり、方法が違う場合があります。
※また、1行目に項目名（ヘッダー）があることを確認してください。
ステップ2：分析ツールを有効にする
Excelの「分析ツール」は初期状態では無効になっています。以下の手順で有効化しましょう。
メニューから 「ファイル」→「オプション」をクリック
開いた状態で左上にある「ファイル」押します。すると画面が変わり、保存とか印刷とかが左に出てきます。一番下に「オプション」があるので、こちらをクリックしてください。
Excelのオプションにある「アドイン」内の「設定(G)…」をクリック
オプション内には数式やデータ等色々ありますが、下のほうに「アドイン」があります。アドイン内の下部にある「管理」欄を「Excelアドイン」にして「設定(G)…」をクリックしてください。
有効なアドイン内の「分析ツール」にチェックを入れ、「OK」をクリック
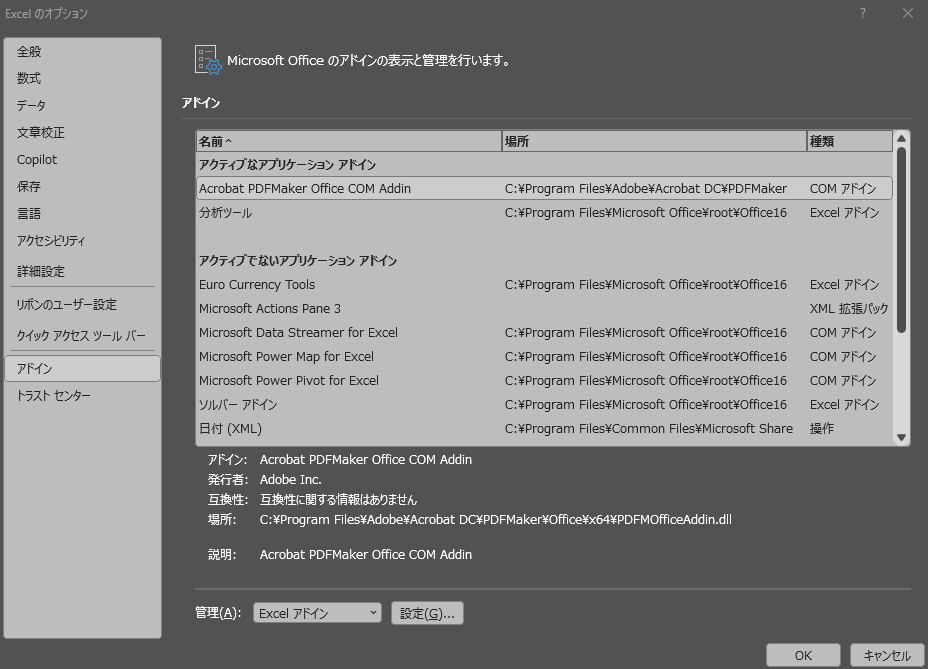
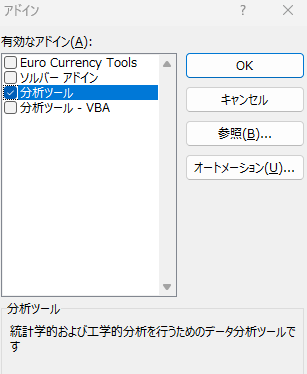
設定内では有効なアドインを選択できると思います。ここで、「分析ツール」を選んでチェックを入れてください。「OK」をクリックすると選択が反映されます。
データタブ内に「データ分析」があれば完了です。
トップ画面に戻り、データタブ内の右側に分析：データ分析のタブが反映されていれば設定完了です。
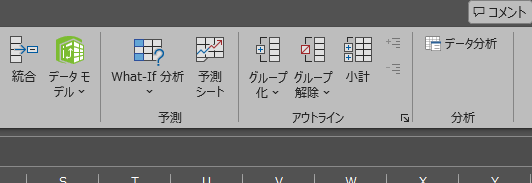
すると、「データ」タブに「データ分析」ボタンが追加されます。
Office 365やExcel for Macでは分析ツールの場所が違うことがあります。バージョンによっては『分析ツール – VBA』も一緒にチェックしてください。
ステップ3：回帰分析を実行する
いよいよ分析開始です！
- 「データ」タブ から「データ分析」をクリック
- 「回帰分析」 を選択 → 「OK」
回帰分析を選択状態にして「OK」をクリックします。
すると、回帰分析用の入力欄として次のような画面が出てきます。
ここでは大きく分けて４つ、さらに詳細な入力欄に分かれています。
- 入力元
- 入力Y範囲
- 入力X範囲
- ラベル
- 定数に０を使用
- 有意水準
- 出力オプション
- 一覧の出力先
- 新規ワークシート
- 新規ブック
- 残差
- 残差
- 残差グラフの作成
- 標準化された残差
- 観測値グラフの作成
- 正規確率
- 正規確率グラフの作成
基本設定
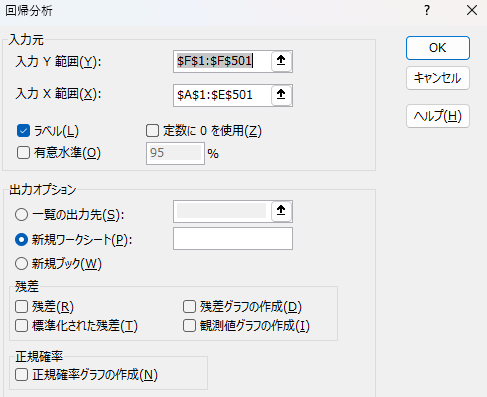
- 以下のように設定します：
- 入力Y範囲：
$F$1:$F$501（目的変数：価格） - 入力X範囲：
$A$1:$E$501（説明変数：面積、部屋数、築年数、駅距離、階数） - 出力オプション：新規ワークシート
- 入力元のラベル（L）：チェック ← 1行目をラベルとして認識
- 入力Y範囲：
詳細オプションの説明
基本的にはチェック不要ですが、知っておくと便利なオプション：
- 残差：実際の価格と予測価格の差を計算
- 残差グラフの作成：予測の精度を視覚的に確認
- 標準化された残差：外れ値（異常なデータ）を発見
- 観測値のグラフ作成：実測値vs予測値の比較グラフ
ステップ4：結果の読み方
分析が完了すると、新しいシートに結果が表示されます。重要なポイントを見ていきましょう。
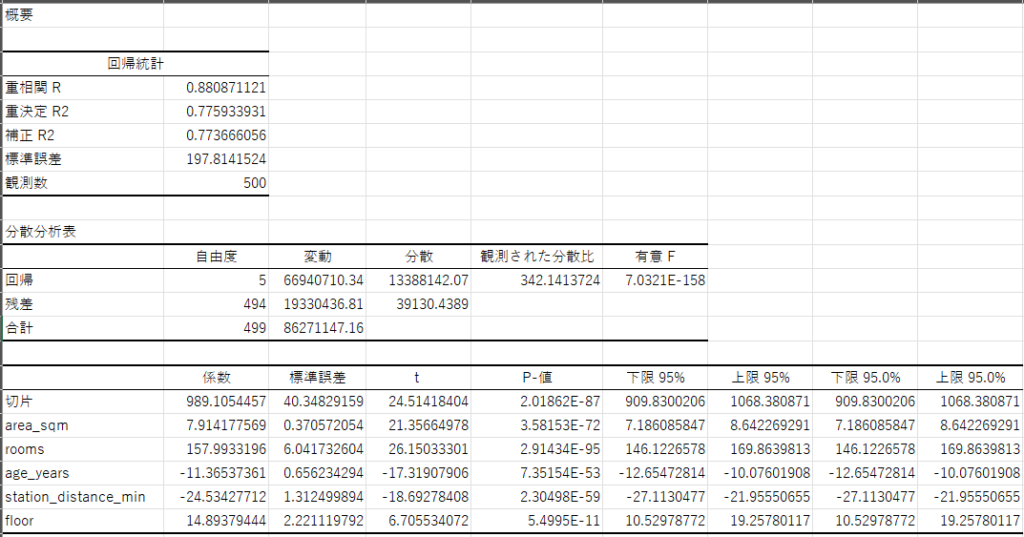
■ 回帰統計
| 指標 | 値 |
|---|---|
| 重相関 R | 0.8809 |
| 重決定 R² | 0.7759 |
| 補正 R² | 0.7737 |
| 標準誤差 | 197.81 |
| 観測数（n） | 500 |
■ 分散分析（ANOVA）
| 分類 | 自由度 | 変動 | 分散 | F値 | 有意確率（P値） |
|---|---|---|---|---|---|
| 回帰 | 5 | 66,940,710.34 | 13,388,142.07 | 342.14 | 7.03 × 10⁻¹⁵⁸ |
| 残差 | 494 | 19,330,436.81 | 39,130.44 | ||
| 合計 | 499 | 86,271,147.16 |
■ 回帰係数と統計量
| 説明変数 | 係数 | 標準誤差 | t値 | P値 | 95%信頼区間（下限） | 95%信頼区間（上限） |
|---|---|---|---|---|---|---|
| 切片（定数） | 989.11 | 40.35 | 24.51 | 2.02 × 10⁻⁸⁷ | 909.83 | 1068.38 |
| area_sqm（面積） | 7.91 | 0.37 | 21.36 | 3.58 × 10⁻⁷² | 7.19 | 8.64 |
| rooms（部屋数） | 157.99 | 6.04 | 26.15 | 2.91 × 10⁻⁹⁵ | 146.12 | 169.86 |
| age_years（築年数） | -11.37 | 0.66 | -17.32 | 7.35 × 10⁻⁵³ | -12.65 | -10.08 |
| station_distance_min（駅距離） | -24.53 | 1.31 | -18.69 | 2.30 × 10⁻⁵⁹ | -27.11 | -21.96 |
| floor（階数） | 14.89 | 2.22 | 6.71 | 5.50 × 10⁻¹¹ | 10.53 | 19.26 |
📊 概要（回帰統計）
一番重要な数値たち：
- 重相関R：0.8809
- 実測値と予測値の相関関係（0〜1の範囲）
- 0.8以上なら「良好」
- 重決定R²：0.7759
- **「このモデルは価格の変動を77.6%説明できる」**という意味
- 0.7以上なら実用的
77.6%って、まあまあなのかな？100%じゃなくて意味ないわけじゃないの…
実は77.6%はかなり優秀なんだ！現実のデータで80%を超えることは珍しく、60%でも実用的とされるくらいだからね。100%だと逆に『データを暗記しただけ』のいわゆる過学習を疑うべきだね。
- 補正R²：0.7737
- 変数の数を考慮した決定係数
- R²とほぼ同じなら過剰適合の心配なし
- 標準誤差：197.81（万円）
- 平均的な予測誤差
- 「大体±200万円の範囲で予測できる」という意味
📈 分散分析表（ANOVA）
- 有意F：7.03E-158（ほぼゼロ）
- モデル全体が統計的に意味があることを示す
- 0.05未満なら合格
🔍 係数表（最も重要！）
各変数が価格に与える影響：
| 変数 | 係数 | 意味 | P値 |
|---|---|---|---|
| 面積 | +の数値 | 1㎡増えると価格上昇 | < 0.05 |
| 部屋数 | +の数値 | 1部屋増えると価格上昇 | < 0.05 |
| 築年数 | -の数値 | 1年古いと価格下落 | < 0.05 |
| 駅距離 | -の数値 | 駅から1分遠いと価格下落 | < 0.05 |
| 階数 | +の数値 | 1階高いと価格上昇 | < 0.05 |
P値が0.05未満なら、その変数の影響は「統計的に有意」（偶然ではない）と言えます。
P値って何？今回はほとんどゼロに近いぐらいな感じみたいだけど。
P値は『偶然でこの結果が出る確率』を表すんだ。だから小さい方がいい。だいたい、0.05（5%）未満なら『偶然じゃない、本当の関係がある』と判断するし、より、厳密にやりたい時は0.01を使うこともあるよ。
📝 結果の解釈
今回の分析結果から分かったこと：
✅ モデルの精度
- 決定係数77.6% → かなり良好な予測精度
- 標準誤差±197万円 → 許容範囲内
✅ 価格に影響する要因
- 面積・部屋数・階数 → プラス影響
- 築年数・駅距離 → マイナス影響
これらは直感的にも納得できる結果ですね！
平均が１７００万円だから、２００万円でも誤差の範囲なんだね。
今回は前処理とかしていないから外れ値に近いものもあったかもしれない。そのようなイレギュラーを無くすとさらに精度がよくなるよ。
💡 実務での活用例
この分析結果を使って：
- 不動産投資：適正価格の判断材料に
- 売却時期の検討：築年数による価格下落の予測
- 物件選び：コスパの良い条件の発見
これで完璧に価格予測できますね！不動産投資で儲けられそう！
ちょっと待ってください！これはあくまで『傾向』を示すもの。立地の詳細、市場の変化、経済情勢など、モデルに含まれない要因もたくさんあります。『参考の一つ』として慎重に活用してくださいね。
まとめ
Excelの「分析ツール」を使えば、プログラミング不要で本格的な統計分析ができます。
今回学んだポイント：
- Excelだけで線形回帰分析は可能
- 決定係数とP値の見方が重要
- 結果の解釈は常識と照らし合わせる
次のステップ：
- 他のデータでも試してみる
- より多くの変数を追加して分析
- 残差グラフで予測精度をチェック
統計分析の第一歩として、ぜひExcelの回帰分析を活用してみてください！
この記事が役に立ったら、ぜひ実際のデータで試してみてくださいね。質問があれば、コメント欄でお気軽にどうぞ！